
In these triangles, the small case letters are the sides and the capital equivalents to those letters represent the angles directly opposite them.
The Sine Rule
If, in a question, you are asked to find an angle in a triangle, and you are given two sides and another angle, you need to use the sine rule for angles.
Let's imagine that you are given a question like this and you have to find the angle:
Use the first diagram and label the sides and their corresponding angles. Here the missing angle would be A and 7cm would be a, as that is the side opposite the missing angle. 81° would be B, meaning that 18cm would be b.
Putting these values in the formula shows us that:
If you are asked to find a missing side in a triangle with two angles and one side, you have to use the sine rule for sides, as illustrated below.
The method used here is similar to the method illustrated above.
The Cosine Rule
If you are given a question where you have to find the missing side given three sides, you would have to use the cosine rule for angles.
Let's imagine you are given a question like this where you had to find the angle:
If the missing angle is A, then 9cm would be a. 10cm would then be b and 11cm would then be c.
Putting these values in the formula shows us that:
If you are asked to find a missing side with two sides and an angle, you would have to use the cosine rule of sides.
The Area of a Triangle
If you have an angle and two sides in a triangle and you are asked to find the area, you have to use this formula:
Putting these values in the formula gives us:


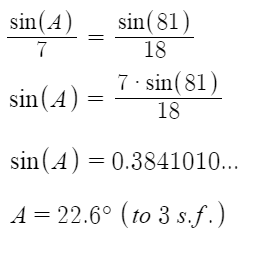







good
ReplyDelete