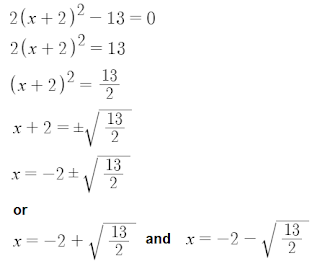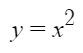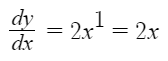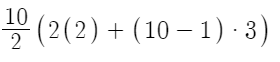The Quadratic Formula

Another way to solve tricky quadratic equations aside from completing the square is by using the quadratic formula.

For example, to solve the below equation, we would have to use the quadratic equation. Some questions will ask you to give your answer to 3 significant figures or in surd form. For the purposes of this example, we will write the answer in surd form.

If you are asked to give the answer to 3 significant figures, the answer would be like below.

Completing the Square

Some quadratic equations cannot be factorised normally, so to factorise such equations, we must complete the square.

To complete the square, equations with an x squared coefficient of 1 should be written in this form:





To complete the square, the x coefficient has to be divided by two. This value would then become the value of p. The value of p has to then be squared and multiplied by -1. This value has to then be added or subtracted from the constant.
Consider this example:

In addition to this, equations with an x squared coefficient not 1 should be written in this form:

The coefficient of x squared has to be divided by the x squared coefficient as well as the x coefficient. Then the square can be completed.
An example is shown below.

Solving equations by completing the square

To solve equations by completing the square, the value of x has to be isolated, or left on its own.

Consider this, from the previous example:

Finding minimum and maximum points by completing the square

The value of x in the completed square which makes the equation in the bracket equal 0 is the x-coordinate of the point, and the value of y is the value of the constant. For example, the minimum point of the second equation is (-2, -13).

Basic Integration

Integration is the reverse of differentiation.

The rule for integration is shown below.

This is the symbol of integration.



This is included because you are integrating with respect to x.


C is the constant of integration. When you differentiate, constants disappear, so lots of functions have the same derivative. When you integrate, the constant is unknown, so you have to write +c at the end.

Consider this equation.

Putting this into the above formula shows us this:

Similar to differentiation, with an equation with many different terms of x, each separate one is integrated separately. For instance:

Basic Differentiation

Say you have a graph with an equation like this:

You can differentiate this equation using the below formula.

In this equation, n is 2, so to differentiate this equation, the number 2 has to be before the x and the power has to be subtracted by 1. So we will get this equation:

means the derivative of y with respect to x.



Differentiating a graph can allow you to find the gradient of a tangent at a certain point. If you replace the x with the x-coordinate of the point in the differentiated equation, you can find the gradient. For example, if we wanted to find the tangent of a graph where x was equal to 2, we would have to substitute 2 for x.

Here the gradient of the tangent at x = 2 is 4.

If you have an equation where different terms of x are added or subtracted, you differentiate each term separately. For example,

You can see how each separate term has been differentiated in this example.

Iterative Methods

To find a root of a quadratic equation accurately, you can use iteration.

Iteration

 Suppose you had a quadratic equation like this and you had to find its root:

You have to rearrange the equation so that only one x value is on the left hand side. Now, some rearrangements of a quadratic equation will not converge to a root, so you would have to rearrange the equation to something different.

Say the equation would be rearranged like below:

The x on the left hand side would be the value of x we need to find, so we can name it xn.
The x on the right hand side is the value of x we use to find the next value of x, so we can name it xn-1.
The equation will then look like this:

The question will sometimes give you a value of x1. If not, you have to input values of x in the original equation and see the value of x where y changes signs.
Here, x1 will be 4. When you find the next value of x, keep on inputting the previous value of x into the formula until the answer rounds to the same number as your previous value (to 3 s.f.).

Binomial Expansion

A binomial expression is the sum or difference of two terms, like x-y, 2a+3b. Expanding (x+1) by the power of 2 is simple, but when it comes to expanding to the power of larger numbers, you need to use other methods. One of the methods is using Pascal's Triangle.

Pascal's Triangle

Pascal's triangle is a special diagram created by Blaise Pascal, where two numbers on a row add up to the number below it.

What's special here is that the rows of numbers are the binomial coefficients.

To expand the binomial expression below, we have to look at the row that begins with 1 and 3, which is 1, 3, 3, 1. As the power of a decreases, the power of b increases.

The power of a goes from 3 to 0, and the power of b goes from 0 to 3.                      

The Binomial Theorem

The theorem is used when the power is large and where Pascal's triangle cannot be used. However, it can enable us to expand to powers of a positive whole number.

2! means 2 factorial, or 2 x 1. 5! = 5 x 4 x 3 x 2 x 1

We will use the binomial theorem to expand this binomial expression.

a will be substituted as 1, b will be x and n will be 2. Putting these values into the binomial theorem shows us that the binomial can be expanded this way.

Pictures from: http://www.mathcentre.ac.uk/resources/uploaded/mc-ty-pascal-2009-1.pdf

Arithmetic Sequences

Arithmetic sequences are sequences where a number is added or subtracted from the previous number to get the next number.

The nth term of an Arithmetic Sequence

The nth term of an arithmetic sequence can be found using this formula, shown in Figure 1.

Figure 1

In this formula, a is the first term, n is the term number and d is the common difference.

Consider this sequence
                                    2, 5, 8, 11,...

Here the first term is 2 and the common difference is 5-2, or 3.

The nth term for this sequence would be:

or, simplified, 3n-1.

The Sum of an Arithmetic Sequence

The sum of and arithmetic sequence can be found using this formula.

In this case, n is the number of numbers being summed.

Consider the previous sequence.
If we had to sum the first ten numbers in this sequence, we would put the values of n, a and d into the formula.

or 155.




Try these questions.

Pictures from: http://www.a-levelmathstutor.com/arithmetic.php
                      http://www.mathcentre.ac.uk/resources/uploaded/mc-ty-apgp-2009-1.pdf

Geometric Sequences

Geometric sequences are sequences where the previous number is multiplied by a certain number to obtain the next number.

The nth term of a Geometric Sequence

The nth term of a geometric sequence is shown in Figure 1.

Figure 1

Here a is the first term in the sequence, r is the common ratio and n is the term number.

Consider the sequence

                                  2, 6, 18, 54, ...

The first term is 2. The common ratio is 6 ÷ 2, or 3. In other words, each term is three times larger than the previous term.

Thus the nth term of this sequence would be 2 x 3^n-1.

The Sum of a Geometric Sequence

The formula to find the sum of a geometric sequence is shown in Figure 2.

Figure 2

The same applies here where a is the first term, r is the common ratio and n is the number of numbers being summed.

Consider the previous sequence.

If we wanted to add up the first ten numbers in the sequence, we would use this formula.

a would be 2, r would be 3 and n would be 10.

Putting these values into the formula shows us that:

The sum of the first ten numbers would then be 59048.

The Sum to Infinity

The sum to infinity of converging sequences can be represented by this formula.

Consider the sequence

                                  1, 0.5, 0.25, 0.125, ...
This sequence tends to 0. The first term is 1 and the common ratio is 0.25 ÷ 0.5, or 0.5.

Putting these values into the formula shows us that:

This shows us that the sum to infinity of this sequence is 2.

Pictures from: http://www.mathcentre.ac.uk/resources/uploaded/mc-ty-apgp-2009-1.pdf